Intersection Over Union (IOU)
Overlap between two bounding boxes (Bgt, Bp)
IOU를 적용함으로써 detection이 valid한지 (True Positive) or not valid한지 (False positive) 말할 수 있음
Bp Bgt 교집합 / Bp Bgt 합집합
True Positive : 맞다고 추측하고 실제로 맞음. IOU >= Threshold
False Positive : 맞다고 추측하고 실제로는 틀림. IOU < Threshold
False Negative : 아니라고 추측하고 실제로는 맞음. Ground Truth를 아예 detect 못함
True Negative : 아니라고 추측하고 실제로 아님.
True negative는 IOU에서 쓰이지 않는 개념임. Corrected misdetection을 반영하기 때문.
잘못된 bounding box들이 여러 개 있는데 걔네를 다 잘못됐다고 했다고..그게 좋은 성능을 가졌다는 것을 나타내지는 않기 때문에 사용하지 않는 개념이다.
보통 IOU의 Threshold로는 50%, 75%, 95% 사용한다.
Precision

적절하게 Detection 하는지. 5000개의 object를 detection했는데 그 중 100개가 진짜인 것과,
100개를 detection 했고 그 중 80개가 맞는 것을 구분하는 지표
Recall

모든 적절한 경우를 찾게 하는 능력을 평가하는 지표
모든 Bgt에 대해 맞게 detectiond 된 gt의 비율로, Bgt가 100개인데 그중 몇개를 잘 detection했는지 분석
Confidence Level
예측한 class 에 대해 어느정도의 확신을 가지고 있는지.
Object Detection의 Popular Metrics
Precision * Recall Curve
Precision은 모든 detection에 대해 맞는 detection이 몇개냐
Recall은 모든 정답값에 대해 몇개나 detection을 했냐
보통의 알고리즘에서는 recall과 precision이 반비례 관계이므로 curve 그렸을 때 1에 가까울수록 좋은거임
특정 class 에 대해 어떤 모델이, recall을 증가시켰을 때 precision이 여전히 좋다면 성능이 좋다고 고려될 수 있음
Precision과 Recall은 다른 방법으로 어떻게 표현할 수 있냐면
0 False Positive == High Precision
0 False Negative == High Recall
성능이 좋지 못한 모델같은 경우 모든 ground truth object 를 찾기 위해 먼저 detected objects의 개수를 늘려야함. 즉 recall을 먼저 상승시켜야 한다.
==> 따라서 보통의 Precision * Recall 그래프는 High Precision Value에서 시작해서 recall을 증가시키는 방향으로 진행됨.
Average Precision
Precision * Recall Curve의 Area Under the Curve (AUC) 를 계산함으로써 performance 계산 가능하다.
AP curve가 보통 지그재그 (위아래로) curve이기 때문에 서로 다른 curve를 비교하는 게 쉽지 않기 때문임. (비교한다 하더라도 두 커브가 쉴새없이 만남… 둘다 지그재그일 경우에)
따라서 Average Precision (AP) 는 서로 다른 모델을 비교하는 데 도움됨
Average Precision: 0~1 사이의 모든 recall 값에 대해 평균을 낸 precision == precision * recall curve의 AUC
11-Point interpolation:
Precision * Recall Curve 모양을 요약하기 위해 나온 개념.
0-1 의 recall을 11등분한 상태에서의 precision을 평균낸 것

with

where
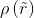
is the measured precision at recall

.
각 point에서 얻어진 precision을 쓰지 않음.
Average Precision은 11 단계 ( 0.0~1.0)의 r에서 precision을 interpolation 하는데 이때 recall value가 r보다 큰 애들 중 max precision을 취해서 interpolating.
Then How to Increase Recall?
Threshold가 0.5라고 했을 때의 Precision, Recall을 구한 후에 Detection 결과의 confidence 값의 threshold를 조절하며 Recall 조절…
잘 와닿지 않음…
==> 링크 참조:
https://datascience.stackex...
BB | confidence | GT
----------------------
BB1 | 0.9 | 1
----------------------
BB2 | 0.9 | 1
----------------------
BB3 | 0.7 | 0
----------------------
BB4 | 0.7 | 0
----------------------
BB5 | 0.7 | 1
----------------------
BB6 | 0.7 | 0
----------------------
BB7 | 0.7 | 0
----------------------
BB8 | 0.7 | 1
----------------------
BB9 | 0.7 | 1
----------------------
이런식의 table이 있을 때 confidence를 기준으로 나열해놓고 BB1, BB1-BB2, BB1-BB3까지의
Precision과 recall을 계속 계산해나가면
rank=1 precision=1.00 and recall=0.14
----------
rank=2 precision=1.00 and recall=0.29
----------
rank=3 precision=0.66 and recall=0.29
----------
rank=4 precision=0.50 and recall=0.29
----------
rank=5 precision=0.40 and recall=0.29
----------
rank=6 precision=0.50 and recall=0.43
----------
rank=7 precision=0.43 and recall=0.43
----------
rank=8 precision=0.38 and recall=0.43
----------
rank=9 precision=0.44 and recall=0.57
----------
rank=10 precision=0.50 and recall=0.71
이렇게 됨.
Accuracy
Object Detection에서는 False를 False라고 예측한 경우는 별 의미가 없으므로… Accuracy가 자주 쓰일지는 몰겠음.
아무튼 True를 True라고 옳게, False를 False라고 옳게 답하는 두 경우 모두 고려하는 게 Accuracy.

이때 domain이 편중되어있다면, 즉 Data의 domian bias가 심하다면 성능 차이가 날 수 있음.
예를 들면 예측하고자 하는 한 달이 매우 맑기만 하고 거의 비오는 날이 아니라면, 비 오는 날 예측하는 성능이 낮을수밖에 없음…
F1 Score
Precision과 Recall의 조화평균
데이터 label이 불균형 구조일때 성능평가 가능


즉, 어떤 비중이 클 때 걔가 끼치는 bias가 줄어든다.
COCO Detection Challenge에서 쓰이는
AP Across Scales, AR Across Scales는 단순히 Object의 Size에 대해 나열한 것이다.
즉 작은 Object부터 큰 Object까지 잘 detection 했냐는 것인데,
Small object(Area < 32^2)에 대한 AP, medium object에 대한 AP 이런 식인 거다.
++ 정확성 뿐 아니라 FPS (Frame Per Second)도 매우 중요한 성능평가 지표.
다만 FPS는 Precision, Recall 등과는 다르게 성능을 평가할 때 사용된 하드웨어 등에 많은 영향을 받기 때문에
항상 절대적인 값이 아니고 상대적인 성능평가 지표라는 것이 단점이다.
'Computer Vision > Deep Learning' 카테고리의 다른 글
| no module named 'tensorflow' error 해결 (0) | 2020.09.27 |
|---|---|
| Gaussian Mixture Model - GMM (0) | 2020.07.09 |
| SNIPER: Efficient Multi-Scale Training (0) | 2020.02.20 |
| Feature Pyramid Network - FPN (0) | 2020.02.18 |


